Stack

Stack is a linear data structure where insertion and deletion of items takes place at one end (i.e. the top), which is known as LIFO - Last In First Out.

Here is a structural definition of stack (which is quite interesting):

A stack is a recursive data structure.
It is either empty or it consists of a top and the rest of which is a stack.

There are three basic operations performed on stack:

• push: add an item to the top of the stack
• pop: remove the item on the top of the stack
• peek: access to the top of the stack

A stack can be implemented through an array or a linked list. The key is to maintain the index of the top element.

public class MyStack<T> {
    private List<T> array;

    public MyStack() {
        array = new ArrayList<>();
    }

    public void push(T obj) {
        array.add(obj);
    }

    public T pop() {
        int e = peek();
        array.remove(array.size() - 1);
        return e;
    }

    public T peek() {
        if (array.isEmpty()) {
            throw new RuntimeException();
        }
        return array.get(array.size() - 1);
    }
}

Applications of stack include:

• DFS and backtracking due to its support for recursion
• evaluating expressions
• undo operations

The rest of this post will be focused on the applications.

Min stack

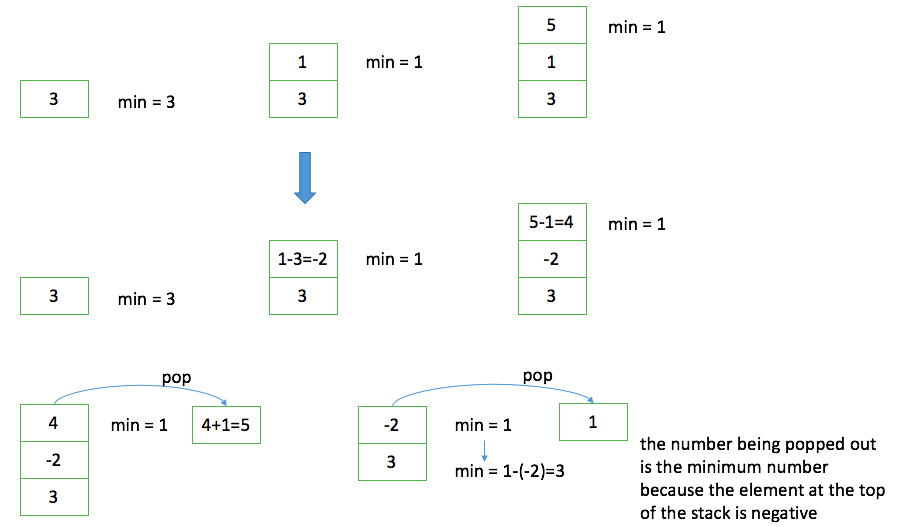
155. Min Stack: design a stack that supports retrieving the minimum element in constant time.

It is an interesting problem. A straightforward solution is to use an extra stack to maintain the minimum element for each new element that is pushed into the stack, but it doubles the space complexity. How can we solve the problem without using extra space?

Instead of storing the raw number in the stack, we can store the difference between the raw number and the current minimum number. The trick is that the difference is negative if the raw number is less than the current minimum number, and this is how we decide whether to update the minimum number when an element is popped out.

public class MinStack {
    private List<Integer> array = new ArrayList<>();
    private int min;

    public void push(int num) {
        array.add(num - min);
        if (num < min) {
            min = num;
        }
    }

    public int pop() {
        if (array.isEmpty()) {
            throw new RuntimeException();
        }
        int num = array.get(array.size() - 1);
        array.remove(array.size() - 1);
        int rawNum = min;
        if (num < 0) {
            min = min - num;
        } else {
            rawNum += num;
        }
        return rawNum;
    }

    public int peek() {
        if (array.isEmpty()) {
            throw new RuntimeException();
        }
        int num = array.get(array.size() - 1);
        int rawNum = min;
        if (num >= 0) {
            rawNum += num;
        }
        return rawNum;
    }

    public int getMin() {
        if (array.isEmpty()) {
            throw new RuntimeException();
        }
        return min;
    }
}

Evaluating expression

To simplify the problem, the expression only contains positive integers, +, -, *, - and ().

An expression can be represented using a binary tree, with the operators as the non-leaf nodes and the operands as the leaf nodes, and brackets are not required in the binary tree. To evaluate an expression, we can start from the leaf nodes and move upwards, exactly the same as we traverse a binary tree according to post-order.

However, maintaining a binary tree is too much in this case. Instead, we can directly convert an expression to a postfix expression (aka. Reverse Polish Notation) and then evaluate the postfix expression.

For example, the postfix expression of (2+3)\(7-4)+9-6/3 is 23+74-*9+63/-*. This can be done by using a queue and a stack - a queue for storing the postfix expression and a stack for storing the operators. It takes only one scan of the expression:

• if it is a number, add it to the queue
• if it is a ‘(‘, push it into the stack
• if it is a ‘)’, pop out the operators from the stack until ‘(‘, and add them to the queue
• if it is a ‘*‘ or ‘/‘, pop out the operators (‘*‘ or ‘/‘) from the stack, and add them to the queue, push the new operator into the stack
• if it is a ‘+’ or ‘-‘, pop out the operators from the stack until ‘(‘, and add them to the queue, push the new operator into the stack

The evaluation of the postfix expression is easy with the help of the stack - a stack for storing the numbers and a stack for storing the postfix expression (because the elements are fetched from the head), but after the conversion the postfix expression is stored in a queue. Do we need to get the elements from the queue and push them into the stack? The answer is no. Let me introduce Deque in Java Collections here. It is a data structure which can be serveed as both a queue and a stack. The evaluation takes only one scan of the postfix stack as well:

• if it is a number, push it into the number stack
• if it is an operand, pop two numbers from the number stack, do the math and then push the result into the number stack
• the number left in the number stack is the final result

Here is an implementation of evaluating an infix expression:

public int evaluate(String expression) {
    // A deque is used here it can be served as both a queue and a stack
    Deque<String> postStack = convert(expression);
    return evaluatePostfix(postStack);
}

private Deque<String> convert(String expression) {
    Deque<String> queue = new ArrayDeque<>();

    Deque<Character> opStack = new ArrayDeque<>();
    int i = 0;
    StringBuilder num = new StringBuilder();
    while (i < expression.length()) {
        char ch = expression.charAt(i++);
        if (ch >= '0' && ch <= '9') {
            num.append(ch);
            continue;
        }
        if (num.length() > 0) {
            queue.add(num.toString());
            num = new StringBuilder();
        }

        switch (ch) {
        case '(':
            opStack.push(ch);
            break;
        case ')':
            while (!opStack.isEmpty() && opStack.peek() != '(') {
                queue.add(String.valueOf(opStack.pop()));
            }
            opStack.pop();
            break;
        case '*':
        case '/':
            while (!opStack.isEmpty()) {
                char op = opStack.peek();
                if (op != '*' && op != '/') break;
                queue.add(String.valueOf(opStack.pop()));
            }
            opStack.push(ch);
            break;
        case '+':
        case '-':
            while (!opStack.isEmpty() && opStack.peek() != '(') {
                queue.add(String.valueOf(opStack.pop()));
            }
            opStack.push(ch);
        }
    }

    if (num.length() > 0) {
        queue.add(num.toString());
    }
    while (!opStack.isEmpty()) {
        queue.add(String.valueOf(opStack.pop()));
    }

    return queue;
}

private int evaluatePostfix(Deque<String> postStack) {
    Deque<Integer> numStack = new ArrayDeque<>();

    while (!postStack.isEmpty()) {
        String s = postStack.pop();
        if (NumberUtils.isNumber(s)) {
            numStack.push(NumberUtils.toInt(s));
        } else {
            int num2 = numStack.pop();
            int num1 = numStack.pop();
            char op = s.charAt(0);
            switch (op) {
            case '+': numStack.push(num1 + num2); break;
            case '-': numStack.push(num1 - num2); break;
            case '*': numStack.push(num1 * num2); break;
            case '/': numStack.push(num1 / num2); break;
            }
        }
    }

    return numStack.pop();
}

As you may notice, the deque for storing post fix expression is an intermediate result. We can save the effort of building such a deque; instead, it is enough for the evaluation to use two stacks - one stack for numbers and the other for operators. The process takes only one scan as well:

• if it is a number, add it to the number stack
• if it is a ‘(‘, push it into the operator stack
• if it is a ‘)’, pop out the operators from the operator stack until ‘(‘, do the math and push the result into the number stack
• if it is a ‘*‘ or ‘/‘, pop out the operators (‘*‘ or ‘/‘) from the operator stack, do the math and push the result into the number stack; push the new operator into the operator stack
• if it is a ‘+’ or ‘-‘, pop out the operators from the operator stack until ‘(‘, do the math and push the result into the number stack; push the new operator into the operator stack

public int evaluate(String expression) {
    Deque<Integer> numStack = new ArrayDeque<>();
    Deque<Character> opStack = new ArrayDeque<>();

    int num = 0;
    boolean pushedNum = false;

    int i = 0;
    while (i < expression.length()) {
        char ch = expression.charAt(i++);
        if (ch >= '0' && ch <= '9') {
            num = num * 10 + (ch - '0');
            pushedNum = true;
            continue;
        }

        if (pushedNum) {
            numStack.push(num);
            num = 0;
            pushedNum = false;
        }

        switch (ch) {
        case '(':
            opStack.push(ch);
            break;
        case ')':
            while (!opStack.isEmpty() && opStack.peek() != '(') {
                numStack.push(calculate(opStack.pop(), numStack.pop(), numStack.pop()));
            }
            opStack.pop();
            break;
        case '*':
        case '/':
            while (!opStack.isEmpty()) {
                char op = opStack.peek();
                if (op != '*' && op != '/') {
                    break;
                }
                numStack.push(calculate(opStack.pop(), numStack.pop(), numStack.pop()));
            }
            opStack.push(ch);
            break;
        case '+':
        case '-':
            while (!opStack.isEmpty() && opStack.peek() != '(') {
                numStack.push(calculate(opStack.pop(), numStack.pop(), numStack.pop()));
            }
            opStack.push(ch);
        }
    }

    if (pushedNum) {
        numStack.push(num);
    }

    while (!opStack.isEmpty()) {
        numStack.push(calculate(opStack.pop(), numStack.pop(), numStack.pop()));
    }

    return numStack.pop();
}

private int calculate(char op, int num2, int num1) {
    switch (op) {
    case '+': return num1 + num2;
    case '-': return num1 - num2;
    case '*': return num1 * num2;
    case '/': return num1 / num2;
    }

    throw new RuntimeException();
}

Valid parentheses

Stack is born for handling problems relating to brackets, like this simple one 20. Valid Parentheses.

Here is a tough one 32. Longest Valid Parentheses, which is worth a try.

My idea is to make use of two stacks:

• Stack1: maintain the index of ‘(‘, if there is a matching ‘)’, then pop this out ‘(‘
• Stack2: maintain the start index and the ending index of the longest valid parentheses; merge the adjacent valid parentheses, e.g. ()(), (())

public int longestValidParentheses(String s) {
    Deque<Integer> stack1 = new ArrayDeque<>();
    Deque<Integer> stack2 = new ArrayDeque<>();

    for (int i = 0; i < s; i++) {
        char ch = s.charAt(i);
        if (ch == '(') {
            stack1.push(i);
        } else {
            if (!stack1.isEmpty() && stack1.peek() + 1 == i) {
                merge(stack2, stack1.pop(), i);
            }
        }
    }

    int max = 0;
    while (!stack2.isEmpty()) {
        int end = stack2.pop();
        int start = stack2.pop();
        if (max < (start - end)) {
            max = start - end;
        }
    }
    return max;
}

private void merge(Deque<Integer> stack, int start, int end) {
    if (stack.peek() + 1 == start) {
        stack.pop();
        stack.push(end);
    } else if (stack.peek() + 1 == end) {
        stack.pop();
        stack.pop();
        stack.push(start);
        stack.push(end);
    } else {
        stack.push(start);
        stack.push(end);
    }
}

I learned from the Discuss-solution-using-a-stack) that it can be solved using only one stack. The idea is to keep the index of the unmatched parathesis in the stack.

public int longestValidParentheses(String s) {
    int left = 0; // this is used for validation of close parathesis
    Deque<Integer> stack = new ArrayDeque<>();
    for (int i = 0; i < s.length(); i++) {
        char ch = s.charAt(i);
        if (ch == '(') {
            stack.push(i);
            left++;
        } else {
            if (left > 0) {
                stack.pop();
                left--;
            } else {
                stack.push(i);
                left = 0;
            }
        }
    }

    int max = 0;
    int end = s.length();
    while (!stack.isEmpty()) {
        int start = stack.pop();
        if (max < (end - start - 1)) {
            max = end - start - 1;
        }
        end = start;
    }
    if (max < end) {
        max = end;
    }

    return max;
}