Find a Number in a Sorted Array

Posted on | In

Given an array of numbers sorted in ascending (or descending) order, a common solution to find a target number is binary search. Binary search starts at the middle position of the array, and narrows down the searching range to half of the array by comparing the target number to the number on the middle position; and then repeats this process until the target number is found or the searching range is left to be 0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// suppose the array of nubmers are sorted in ascending order
int binarySearch(int[] array, int target) {
    int i = 0;
    int j = array.length - 1;
    while (i <= j) {
        int mid = (i + j) / 2;
        if (target == array[mid]) return mid;
        if (target < array[mid]) {
            j = mid - 1;
        } else {
            i = mid + 1;
        }
    }
    return -1;
}

Time complexity: O(log(n)).

There are a variety of interesting problems which are derived from this simple searching problem. In Part I, I’ll go through such searching problems confined to an array. In Part II, the problems are focused on the matrix.

I. Find a number in an array

i. Search for a range

34. Search for a Range: given an array of integers sorted in ascending order, find the starting and ending position of a target number (the array may contain duplicates).

Solution 1: find the target number in the array using binary search, and then go through its neighbors on the left until finding the starting position, and go through its neighbors on the right for the ending position. Time complexity is O(log(n) + k), k is the number of the target element.

Solution 2: find the starting position of the target using binary search, and then find the ending position using binary search as well. Time complexity is O(log(n)).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// find the starting position
int i = 0;
int j = array.length - 1;
while (i <= j) {
    int mid = (i + j) / 2;
    if (target == array[mid]) {
        if (mid == 0 || array[mid] != array[mid - 1]) return mid;
        j = mid - 1;
    } else if (target < array[mid]) {
        j = mid - 1;
    } else {
        i = mid + 1;
    }
    return -1;
}

ii. The sorted array is rotated

33. Search in Rotated Sorted Array: find the target number in an array which is sorted in ascending order but rotated at some pivot (no duplicate exist in the array).

The solution is binary search with a little change on narrowing down the searching range. It cannot decide the target is on the left side or the right side by simply comparing the target number to the number on the middle position.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int i = 0;
int j = nums.length - 1;
while (i <= j) {
    int mid = (i + j) / 2;
    if (target == nums[mid]) return mid;
    if (nums[i] < nums[j]) { // if numbers in array[i..j] are in ascending order
        if (target < nums[mid]) {
            j = mid - 1;
        } else {
            i = mid + 1;
        }
    } else { // if numbers in array[i..j] are rotated
        if (nums[mid] > nums[j]) { // if numbers in array[i..mid] are in ascending order
            if (target >= nums[i] && target < nums[mid]) {
                j = mid - 1;
            } else {
                i = mid + 1;
            }
        } else { // if numbers in array[mid..j] are in ascending order
            if (target > nums[mid] && target <= nums[j]) {
                i = mid + 1;
            } else {
                j = mid - 1;
            }
        }
    }
}
return -1;

Follow-up: what if the array contains duplicates?
81. Search in Rotated Sorted Array II: find out if a given number exists in the array.

For the case when nums[i] == nums[mid] && nums[mid] == nums[j], it cannot tell if the numbers in nums[i..mid] are the same or the ones in nums[mid..j] are the same (e.g. {1, 1, 3, 1} vs. {1, 3, 1, 1, 1}), and hence it cannot narrow down the searching range by half. The time complexity should be a little more than O(log(n)).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int i = 0;
int j = nums.length - 1;
while (i <= j) {
    int mid = (i + j) / 2;
    if (target == nums[mid]) return true;
    if (nums[i] < nums[j]) {
        if (target < nums[mid]) {
            j = mid - 1;
        } else {
            i = mid + 1;
        }
    } else {
        if (nums[mid] < nums[j]) {
            if (target > nums[mid] && target <= nums[j]) {
                i = mid + 1;
            } else {
                j = mid - 1;
            }
        } else if (nums[mid] > nums[j]) {
            if (target < nums[mid] && target >= nums[i]) {
                j = mid - 1;
            } else {
                i = mid + 1;
            }
        } else { 
            if (nums[mid] != nums[i]) {
                j = mid - 1;
            } else { // if nums[mid]==nums[j] && nums[mid]==nums[i]
                i++;
                j--; // cannot tell if it is {1, 1, 3, 1} or {1, 3, 1, 1, 1}
            }
        }
    }
}
return false;

153. Find Minimum in Rotated Sorted Array: find the minimum number in an array which is sorted in ascending order but rotated at some pivot (no duplicate exist in the array).

Instead of finding a target number in an array, this problem is finding the number which is smaller than its left neighbor or the first number if the whole array is in ascending order. We can narrow down the searching range by ruling out the half part which is in ascending order unless the whole array is in ascending order.

1
2
3
4
5
6
7
8
9
10
11
12
13
int i = 0;
int j = nums.length - 1;
while (i <= j) {
    int mid = (i + j) / 2;
    if (nums[i] < nums[j]) return i;
    if (mid > 0 && nums[mid] < nums[mid - 1]) return mid;
    if (mid < nums.length - 1 && nums[mid] > nums[mid + 1]) return mid + 1;
    if (nums[mid] > nums[i]) { // if array[i..mid] is in ascending order
        i = mid + 1;
    } else { // if array[mid..j] is in ascending order
        j = mid - 1;
    }
}

Be aware of these test cases (when mid equals to i):

1
2
{1, 2}
{2, 1}

Follow-up: what if the array contains duplicates?
154. Find Minimum in Rotated Sorted Array II: find the minimum number.

Be aware of the situation when nums[mid] equals to nums[j] and nums[mid] equals to nums[j], e.g. {1, 1, 3, 1}, {1, 3, 1, 1, 1}.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int i = 0;
int j = nums.length - 1;
while (i < j) {
    int mid = (i + j) / 2;
    if (nums[i] < nums[j]) { break; }
    if (mid > 0 && nums[mid] < nums[mid - 1]) { i = mid; break; }
    if (mid < nums.length - 1 && nums[mid] > nums[mid + 1]) { i = mid + 1; break; }
    if (nums[mid] > nums[i]) { // if array[i..mid] is in ascending order
        if (nums[mid] <= nums[j]) break;
        i = mid + 1;
    } else if (nums[mid] < nums[i]) { // if array[mid..j] is in ascending order
        j = mid - 1;
    } else {
        if (nums[mid] == nums[j]) {
            j--;
        } else {
            i = mid + 1;
        }
    }
}
return i;

iii. Search for duplicate number

287. Find the Duplicate Number: find the only one duplicate number in an array containing n + 1 integers where each integer is between 1 and n(inclusive).

Since it is required to use O(1) extra space only, we cannot keep a counter for each number in the array. A straightforward way is using brutal force to find the duplicate number, and the time complexity is O(n^2).
You may wonder how to apply binary search to this problem. The array is not sorted, so a little twist is needed here. Instead of directly use binary search on the array, we can use binary search on the number n. If there are more than k elements between i and i+k-1 (inclusive) in the array, the duplicate number must be in this range, so we can narrow down the searching range from 1 ~ n to i ~ i+k-1. The time complexity is O(n*log(n)).

1
2
3
4
5
6
7
8
9
10
11
12
int i = 1;
int j = n;
while (i < j) {
    int mid = (i + j) / 2;
    int k = countNumberNoMoreThanMid(nums, mid);
    if (k <= mid) { // note that for this case {2, 2, 2, 2}, when mid=1, k will be 0
        i = mid + 1;
    } else {
        j = mid;
    }
}
return i;

Here is another solution using two pointers.

II. Find a number in a matrix

Things become more complex when searching a matrix.

74. Search a 2D Matrix: search a target number in a sorted matrix.

If we put the first number in a row after the last number in the previous row, the matrix can be treated as a sorted array, so we can directly apply binary search to this problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
int i = 0;
int j = row * col - 1;
while (i <= j) {
    int mid = (i + j) / 2;
    int num = matrix[mid / col][mid % col];
    if (target == num) return true;
    if (target < num) {
        j = mid - 1;
    } else {
        i = mid + 1;
    }
}
return false;

Follow-up: 240. Search a 2D Matrix II.

For this problem, the matrix cannot be treated as sorted array, but we still can apply the binary search to each row.

But here is a better solution. Let’s start the search at the right top postion (or the left bottom position), if the target is larger than the number on the position, the numbers on the same row can be ruled out because they are all smaller than the target; if the target is smaller, the numbers on the same column can be ruled out. In this way, we can narrow down the searching range as much as possible, and the time complexity is O(row + col).

1
2
3
4
5
6
7
8
9
10
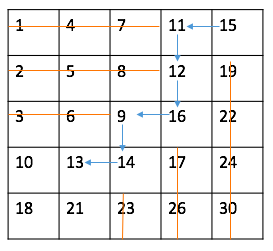
11
int i = 0;
int j = col - 1;
while (i < row && j >= 0) {
    if (target == matrix[i][j]) return true;
    if (target > matrix[i][j]) {
        j++;
    } else {
        i--;
    }
}
return false;

More

378. Kth Smallest Element in a Sorted Matrix: find the kth smallest element in the matrix, given that each of the rows and columns are sorted in ascending order.

One solution is to use a k maximum heap to keep track of the small elements while traversing the matrix.

The other solution is to use binary search. The searching space is the range between the left top number in the matrix to the bottom right number. The key is how to narrow down the searching range. Here is the implementation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int search(int[][] matrix, int k) {
    int vLeft = matrix[0][0];
    int vRight = matrix[n - 1][n - 1];
    while (vLeft < vRight) {
        int vMid = (vLeft + vRight) / 2;
        int count = countLessOrEqual(vMid, matrix);
        if (count < k) {
            vLeft = vMid + 1;
        } else {
            vRight = vMid;
        }
    }
    return vLeft;
}

Quick questions:

  1. Why the condition of termination is vLeft == vRight?
  2. Why vLeft is an element in the matrix?
  3. Why vLeft is the kth smallest element in the matrix?

Here is the answer to the questions. When count is equal to k, it does not return vMid as the result because vMid may be some number larger than the kth smallest element, and it just narrows down the searching range until vMid is the kth smallest element (vMid is always less than or equal to vRight, so the searching ranged will continue to be narrowed down if vMid is not the kth smallest element). When vMid is the kth smallest element, vRight will be become the kth smallest elment for the following loops. Until now, vLeft may be equal to or not equal to vRight. If vLeft is not equal to vRight, vMid will be less than the kth smallest element and hence the count will be less than k, so eventually vLeft will be equal to vRight.

Follow-up: 719. Find K-th Smallest Pair Distance, given an integer array, return the k-th smallest distance among all the pairs.

A straightforward solution is to calculate all the distances and use a maximum heap to find out the k-th smallest one.

Here is another solution which uses binary search.

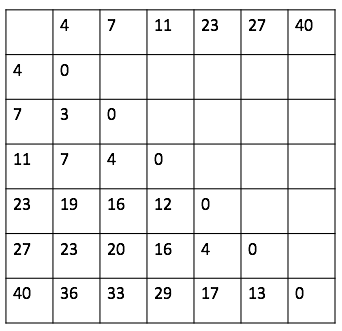
Given an array {4, 11, 40, 23, 7, 27}, if we sort it in ascending order, we can get a sorted matrix of distance as the diagram below, and we can apply the above solution to this problem.