BFS

Posted on | In

BFS, short for Breadth First Search, is an algorithm of searching tree or graph data structures. It starts at some specific nodes and explores the neighbor nodes first before moving to the next level, until it searches through the whole graph.

BFS usually works with a queue.

1
2
3
4
5
6
7
8
9
10
11
// initialize
queue.add(node);
// search
while (!queue.isEmpty()) {
    // Node represents a node in a graph
    Node node = queue.poll();
    // explore the neighbor nodes
    for (Node neighbor : neighbors) {
        if (isQualified(neighbor)) queue.add(neighbor);
    }
}

BFS and DFS are two typical algorithms of searching graphs, and some searching problems can be solved by Union Find as well, so first I want to discuss the scenarios where we should use BFS, DFS or Union Find. And then I will walk through some problems, if they can be solved using DFS or Union Find, I’ll provide the corresponding solutions; otherwise, I’ll list the reasons why DFS or Union Find cannot be applied to the problems.

BFS vs. DFS

The example below compares the way of how BFS traverses and the way of how DFS traverses, assuming that the moving directions can be right and down only.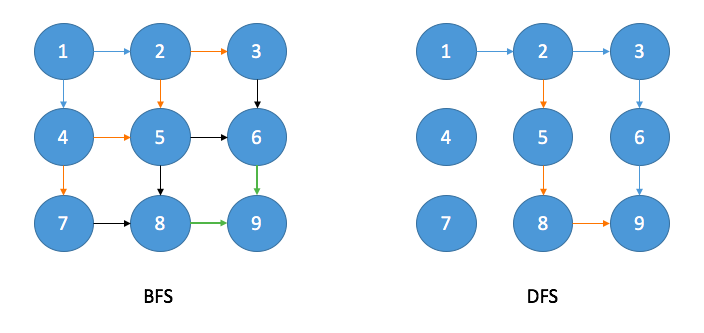
BFS vs. DFS

Sometimes BFS and DFS can be used to solved the same problems. Whether BFS or DFS is a better choice, it depends.

BFS vs. Union Find

Union Find is not a searching algorithm. It partitions a set of elements into a number of non-overlapping subsets. Each element is intialized as a subset of its own, and then subsets are merged if they are of the same kind until the subsets are not overlapping. Although it is quite different than BFS, sometimes they can be used to solve the same problems.

Problems and solutions

i. Binary tree

Level order traversal of binary trees is an example of BFS. See more in this post about binary tree.

ii. Graph

542. 01 Matrix：given a matrix which consists of 0 and 1, find the distance of the nearst 0 for each cell.

BFS solution

Start from all the cells of 0, and explores its adjacent cells, if it is 1 and has not been processed, then update the cell’s distance to be current cell’s distance plus 1 and put it in the queue. Because the search starts from 0, the cells of 1 close to 0 must be processed before those far away from 0.
Time complexity: O(row * col).

1
2
3
4
5
6
7
8
9
10
11
12
// initialize the queue with cells of 0
init(queue, matrix);
int[][] distance = new int[row][col];
while (!queue.isEmpty()) {
    Node cell = queue.poll();
    for (Node neighbor : getNeighbors(cell)) {
        if (neighbor.value == 1 && distance[neighbor.row][neighbor.col] == 0) {
            distance[neighbor.row][neighbor.col] = distance[cell.row][cell.pol] + 1;
            queue.add(neighbor);
        }
    }
}

DFS solution

Since this problem is about finding the shortest distance from 1, DFS has to start from the cells of 1 adjacent to 0, and then it updates the distance of each 1 on the searching path if the length of the path is the shortest until it cannot find any cells which meet the update requirements. The time complexity is O(row * col * k) where k depends on the length of the searching paths.
BFS is a better solution for this problem.

1
2
3
4
5
6
7
8
9
10
11
private void dfs(int i, int j, int dist, int row, int col, int[][] matrix, int[][] updated) {
    int[][] neighbors = getNeighbors(i, j, row, col);
    for (int k = 0; k < neighbors.length; k++) {
        int nI = neighbors[k][0];
        int nJ = neighbors[k][1];
        if (nI > -1 && nJ > -1 && matrix[nI][nJ] == 1 && dist + 1 < updated[nI][nJ]) {
            updated[nI][nJ] = dist + 1;
            dfs(nI, nJ, dist + 1, row, col, matrix, updated);
        }
    }
}

Union Find solution

This problem cannot be handled by the Union Find algorithm, because the union of the matrix cells cannot solve the problem.

iii. Graph

417. Pacific Atlantic Water Flow.

BFS solution

It is obvious that the cells on the top right corner and bottom left corner are where water can flow to both the Pacific ocean and Atlantic ocean, the cells on the first row and first column are where water can flow to the Pacific ocean, and the cells on the last row and last column are where water can flow to the Atlantic ocean, so these are the cells to begin with in a search. If a cell is no higher than its neighbor cell, which means water can flow from the neighbor cell to the current cell, its neighbor cell’s status might need to be updated according to the status of current cell; and if the neighbor cell’s status is updated, it should be put into the queue because the update might affect its surrounding cells’ status.
For each cell, its status will be updated at most twice, so the time complexity is O(m * n).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[][] mark = new int[m][n];
// cells in the first row and first column are initialized as 1 for Pacific
// cells in the last row and last column are initialized as 2 for Atlantic
// [0, n-1] and [m-1, 0] are initialized as 3 for both Pacific and Atlantic
// put these initialized cells in the queue
init(mark, matrix, queue);
while (!queue.isEmpty()) {
    Node node = queue.poll();
    for (Node neighbor : getNeighbors(node)) {
        if (node.height <= neighbor.height) {
            boolean updated = updateMark(neighbor, node);
            if (updated) { queue.put(neighbor); }
        }
    }
}

DFS solution

The key of DFS is to know which cells to start a search and the ending conditions for each search.
Both BFS and DFS are proper solutions for this problem. There is no difference in time complexity.

1
2
3
4
5
6
7
8
9
// cells to start a DFS
for (int i = 0; i < row; i++) {
    dfs(i, 0, row, col, matrix, mark);
    dfs(i, col - 1, row, col, matrix, mark);
}
for (int j = 1; j < col - 1; j++) {
    dfs(0, j, row, col, matrix, mark);
    dfs(row - 1, j, row, col, matrix, mark);
}
1
2
3
4
5
6
7
8
9
10
11
12
private void dfs(int i, int j, int row, int col, int[][] matrix, int[][] mark) {
    int[][] d = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    for (int k = 0; k < d.length; k++) {
        int nI = i + d[k][0];
        int nJ = j + d[k][1];
        if (nI >= 0 && nI < row && nJ >= 0 && nJ < col && matrix[i][j] <= matrix[nI][nJ]
                && mark[nI][nJ] != (mark[i][j] | mark[nI][nJ])) {
            mark[nI][nJ] = mark[i][j] | mark[nI][nJ];
            dfs(nI, nJ, row, col, matrix, mark);
        }
    }
}

Union Find solution

For this problem, Union Find is not a proper solution because a cell marked for “Pacific” can be changed to “Pacific-Atlantic” later and yet Union is just a process of merging without moving one element from one subset to another.

iv. Graph

130. Surrounded Regions: given a 2D board containing ‘X’ and ‘O’, capture all regions surrounded by ‘X’.

BFS solution

If an ‘O’ is at the edges, it cannot be captured, so we can start from the ‘O’s at the edges, and mark other ‘O’s which are connected to these ‘O’. The ‘O’s left are the ones which are captured.
The time complexity depends on the number of ‘O’, so it is O(n) suppose the matrix contains n elements.

1
2
3
4
5
6
7
8
9
10
11
// put all the 'O's at the edges in the queue
init(queue, matrix);
while (!queue.isEmpty()) {
    Node node = queue.poll();
    for (Node neighbor : getNeighbors(node)) {
        if (neighbor.value == 'O') {
            matrix[neighbor.row][neighbor.col] = 'A';
            queue.add(neighbor);
        }
    }
}

DFS solution

The idea is similar to BFS, also starting from all ‘O’s at the edges and marking all the ‘O’s on the path until ‘X’ is encountered. The time complexity is O(n).

1
2
3
for (Node node : nodeAtEdges) {
    dfs(node, matrix);
}
1
2
3
4
5
6
7
8
private void dfs(Node node, char[][] matrix) {
    for (Node neighbor : getNeighbors(node)) {
        if (neighbor.value == 'O') {
            matrix[neighbor.row][neighbor.col] = 'A';
            dfs(neighbor, matrix);
        }
    }
}

Union Find solution

There are two kinds of ‘O’ in this problem, those are surrounded by ‘X’ and those aren’t. Initially, each ‘O’ is the root of its own subset. During the process, if two cells are adjacent but they belong to different subsets, those two subsets are merged. In the end, what we have is that all the ‘O’s are divided into different subsets, some are surrounded by ‘X’ and the others aren’t. So we only need to change all the ‘O’s in the subsets whose root is not at the edge.
The time complexity is O(k * n), where k depends on the time complexity of the Find function.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int[] parent = new int[row * col];
for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j++) {
        if (matrix[i][j] == 'X') continue;
        int root = find(i, j, parent);
        for (Node neighbor : getNeighbors(i, j)) {
            int nI = neighbor.row;
            int nJ = neighbor.col;
            if (matrix[nI][nJ] == 'X') continue;
            int nRoot = find(nI, nJ, parent);
            if (root != nRoot) {
                // union
                if (isAtEdge(root)) {
                    parent[nRoot] = root;
                } else {
                    parent[root] = nRoot;
                }
            }
        }
    }
}
for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j++) {
        if (matrix[i][j] == 'X') continue;
        int root = find(i, j, parent);
        if (!isAtEdge(root)) {
            matrix[i][j] = 'X';
        }
    }
}

v. Graph

200. Number of Islands: count the number of islands; an island is surrounded by ‘0’s and is formed by connecting adjacent ‘1’s.

BFS solution

Start from any ‘1’ that has not been processed, explore the ‘1’s that can form an island and mark them as processed.
Time complexity is O(n), suppose the matrix contains n elements.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int countIslands(char[][] matrix) {
    int counter = 0;
    int[][] mark = new int[row][col];
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            if (matrix[i][j] == '1' && mark[i][j] = 0) {
                mark[i][j] = 1;
                bfs(i, j, mark, matrix);
                counter++;
            }
        }
    }
}

void bfs(int i, int j, int[][] mark, char[][] matrix) {
    queue.add(new Node(i, j));
    while (!queue.isEmpty()) {
        Node current = queue.poll();
        for (Node neighbor : getNeighbors(node)) {
            if (matrix[neighbor.row][neighbor.col] == '1' 
                && mark[neighbor.row][neighbor.col] == 0) {
                mark[neighbor.row][neighbor.col] = 1;
                queue.add(neighbor);
            }
        }
    }
}

DFS solution

The idea is similar to BFS - start from any ‘1’ that has not been processed, explore the ‘1’s that can form an island and mark them as processed. It is that only the way of search differs.
The time complexity is O(n) as well.

1
2
3
4
5
6
7
8
9
// the function bfs() above can be replaced by this function
void dfs(Node node, int[][] mark, char[][] matrix) {
    for (Node neighbor : getNeighbors(node)) {
        if (matrix[neighbor.row][neighbor.col] == '1' && mark[neighbor.row][neighbor.col] == 0) {
            mark[neighbor.row][neighbor.col] = 1;
            dfs(neighbor, mark, matrix);
        }
    }
}

Union Find solution

For the cells that form an island, they belong to the same subset. So the solution is to apply the Union Find algorithm to this problem and then find out how many subsets are there.
The time complexity is O(k * n), where k depends on the find function.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int[] parent = new int[row * col];
for (int i = 0; i < row; i++) {
    for (int j = 0; j < col; j++) {
        if (matrix[i][j] == '0') continue;

        int root = find(i, j); // find
        for (Node neighbor : getNeighbors(i, j)) {
            int nI = neighbor.row;
            int nJ = neighbor.col;
            if (matrix[nI][nJ] == '0') continue;
            int nRoot = find(nI, nJ); // find
            if (root != nRoot) {
                parent[root] = nRoot; // union
            }
        }
    }
}

Follow-up: Numbers of Islands II.

The Union Find algorithm is more suitable for solving this problem. For each operation, we only need to check the four adjacent cells of the new position and then count the number of subset. But if we use BFS or DFS, the time complexity will become unacceptable for it depends on the number of operations.

vi. Other

127. Word Ladder: given two words beginWord and endWord, and a dictionary’s word list, find the length of shortest transformation from beginWord to endWord.

This is similar to Problem ii, so BFS is a better choice for this problem.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Queue<String> queue = new LinkedList<>();
queue.add(endWord);
int count = 0;
int round = 1;

while (count > 0) {
    int tmpCount = 0;
    for (int i = 0; i < count; i++) {
        String word = queue.poll();
        if (word.equals(endWord)) {
            return round;
        }

        List<String> transformedWords = getTransformedWords(word);
        queue.addAll(transformedWords);
        tmpCount += transformedWords.size();
    }
    count = tmpCount;
    round++;
}

return 0;

Suppose there are n words on the list, the time complexity is O(k * n), where k depends on the performance of getTransformedWords().

The function getTransformedWords() can be implemented by precomputation - computing all the transformed words for each word on the list. The time complexity for this implementation is O(n * n), so the overall time complexity is O(n * n);

There is another implementation - stored all the words in a set, so it is easy to verify if a word is valid; get a word’s transformed words by changing one letter at a time and verify their validation using the set. The time complexity is O(k * word’s length), where k depends on the range of the letters.

Follow-up: 126. Word Ladder II, find all the shortest transformation sequence(s).

I cannot think of a solution using BFS only. BFS can be used to get the length of the shortest tranformation, but I have no idea how to get all the possibilities through BFS. However, if I know the minimum length, I can use DFS to get all the possibilities which have the minimum length.

Here is the solution combining BFS and DFS:

  1. Get the length of the shortest tranformation using BFS
  2. Get all the possibilities using DFS, dropping the ones which are longer than the minimum length

After I wrote the code, I realized that the second part wasted a lot of time on useless calculation. For example, “hit -> hot -> got -> …” proves to be invalid, but when backtracking, the program goes through “hit -> hot -> lot -> got -> …” for nothing.

Here is the improved solution:

  1. Get the length of the shortest tranformation from beginWord and all the words on the list to endWord using BFS
  2. Get all the possibilities using DFS, dropping the ones which are longer than the minimum length as soon as possibile