Let’s say, A wants to send a secret message to B. Hypothetically, A owns a key which is also owned by B. Thus, A can encrypt the message using the key and then B can decipher the encoded message using the same key. This is known as symmetric cryptography.
In contrast, asymmetric cryptography doesn’t require A and B to share the same private key; instead, A and B hold two different keys - one public key and one private key (it is impossible to compute the private key based on the public key). If A wants to send a secret message to B, A can first get a public key from B and use it to encode the message, and then B can decode the ciphertext using the private key.
In summary, symmetric cryptography
uses the same cryptographic keys for both encryption of plaintext and decryption of ciphertext.
Asymmetric cryptography
uses public and private keys to encrypt and decrypt data; either of the keys can be used to encrypt a message, and the other key can be used for decryption.
Both cryptography can be used for data confidential, as shown in the example above. Besides, asymmetric cryptography can be applied in other scenarios, like representing the authentication of digital messages (aka. digital signature).
Digital signature using asymmetric cryptography
Suppose that A wants to make sure that a message is sent by B and is not altered in transit, how can asymmetric cryptography help in this case?
This is how it works:
- B generates a pair of keys - one private key and one public key
- B generates the digest of the message using some hashing algorithm and then encrypts the digest using the private key - the encoded digest is known as a digital signature
- B sends the message along with the digital signature and the public key to A
- A decrypts the digital signature using the public key and gets the message digest, which proves that B signs this message (because B is the only one who owns the private key to encrypt the digest)
- A generates the digest of the message using the same hashing algorithm and compares it with the one decrypted from the digital signature, if both digest are equal, then the message has not been tampered in transit.
Flaws in asymmetric cryptography
Asymmetric cryptography is vulnerable to Man-In-The-Middle attacks. Suppose that C (as the man in the middle) has the ability of intercepting the messages between A and B and sending fake messages to A and B, so C can pretend to be A for B and pretend to be B for A, and yet Both A and B are aware of the attack.
Here is an illustration:
- B generates a pair of keys and sends the public key PK1 to A
- C intercepts PK1, but sends a fake one PK1’ to A
- A encrypts a message using PK1’
- C intercepts the message from B and decrypts it using the correspongding private key, then C encrypts the message using PK1 and sends it back to B
- B gets the message and is able to decrypts it.
Why does such an attack work? Because B (who receives the public key) is unable to tell if the public key is authentic.
The most common solution to this problem is to introduce third-party authorities which issue certificates to web servers for authentication. Such an authority is known as a Certificate Authority (CA). Simly speaking, a public key is sent along with a certificate issued by a CA; if the certificate is valid and we trust the CA, we can conclude that the public key is authentic.
The next question is: how do we know if the certificate is valid and if we can trust a specific CA?
Digital certificate
Let’s first get an impression of what a certificate looks like: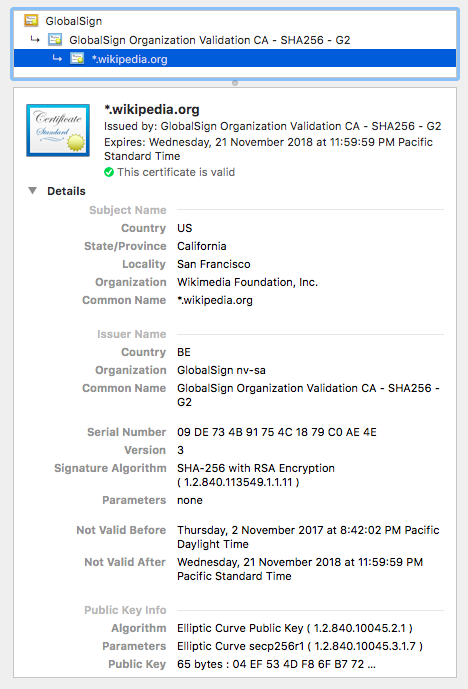
A public key certificate usually contains (most certificates today follow the X.509 v3 structure):
- information about the subject (i.e. the owner of the certificate)
- information about the certificate issuer (aka. CA)
- information about the public key
- fingerprint (i.e. digital signature of the certificate)
This is how a certificate is generated by the CA:
- Put the information about the subject, the issuer, and the public key together and create a certificate
- Generate the digest of the information using some hashing algorithm
- Generate the digital signature by encoding the digest using the private key owned by the issuer
- Attach the digital signature to the certificate.
This is how a certificate is verified:
- Extract the digital signature from the certificate
- Decipher the digial signature using the CA’s public key to get the digest d1
- Apply the same hashing algorithm on the certificate to get the digest d2
- If d1 matches d2, then the certificate is valid and the public key extracted from it can be trusted.
You might wonder where to get the CA’s public key. Let’s get back to the snapshot above. It shows that the issuer is “GlobalSign Organization Validation CA - SH256 - G2”; from here we can get its certificate which contains its public key. Note that the certificate is issued by “GlobalSign”, so it needs the public key of “GlobalSign” to verify the validation of the intermediate CA. “GlobalSign” is a root CA, which means that its certificate can be included on the list of trust and explicitly trusted; “GlobalSign Organization Validation CA - SH256 - G2” is an intermediate CA, so its certificate is not valid unless it is trusted by a trust root CA. So we might get the certificate of “GlobalSign” from the trust store (e.g. keychains on MAC) or a warning message from the browser.
This is known as chain of trust which is well explained in the following diagram.
The whole solution looks perfect except that it is still vulnerable if a trust root CA does not play the game by the book (CNNIC and WoSign are two examples).
The public key certificates and the certificate authorities are part of a system know as Public Key Infrastructure (PKI), but this topic will be left for the future.
References
1 Wikipedia - Symmetric-key Algorithm
2 Asymmetric Cryptography
3 Wikipedia - Public Key Certificate
4 Wikipedia - Public Key Infrastructure
5 What is Digital Signature